Ecological Archives E096-209-A1
Casey P. terHorst, Jennifer A. Lau, Idelle A. Cooper, Kane R. Keller, Raffica J. La Rosa, Anne M. Royer, Elizabeth H. Schultheis, Tomoi Suwa, and Jeffrey K. Conner. 2015. Quantifying nonadditive selection caused by indirect ecological effects. Ecology 96:2360–2369. http://dx.doi.org/10.1890/14-0619.1
Appendix A. Description of a simulation model of the effects of multiple herbivores on selection on plant defensive structures, including supplementary figures.
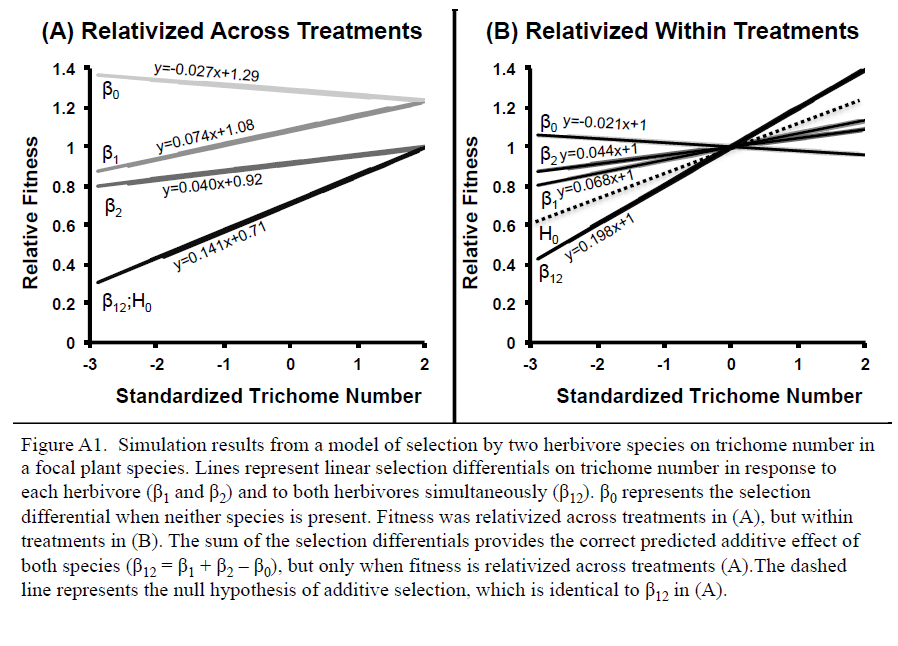
We tested our proposed null expectation using a simple simulation model of species selecting on traits independently and additively (see accompanying supplement file). In our simulation, two herbivore species feed on the same plant species and are deterred by the same plant defensive trait (trichome number). We created a plant population consisting of 99 plants with a normal distribution of trichome numbers (mean = 50, standard deviation = 10). We modeled attack by herbivores on each plant by assuming that trichomes influence the amount of leaf material consumed by each herbivore species in a deterministic fashion, such that the percent leaf damage from Herbivore 1 is 100 – trichome number and the percent leaf damage from herbivore species 2 is 100 – (0.5 × trichome number). That is, trichome defenses are 50% less effective in reducing attack from Herbivore 2 relative to Herbivore 1. Note that damage by each herbivore is independent of damage by the other herbivore. In the absence of herbivores, plants produce a maximum of 1000 seeds. We include costs of trichome production in the absence of herbivores by reducing seed production by 2x number of trichomes. Leaf damage by each of the two herbivores has equal and independent fitness effects—one unit of damage from each herbivore reduces seed production by five seeds regardless of the level of damage by the other herbivore. We estimated linear variance standardized selection differentials by regressing relative fitness (each individual fitness value divided by mean fitness) on standardized trichome number (Lande and Arnold 1983). Previous work has relativized fitness either across all treatments, dividing by the grand mean fitness, or within each treatment, dividing by mean fitness within each treatment; here we evaluated both methods (see below).
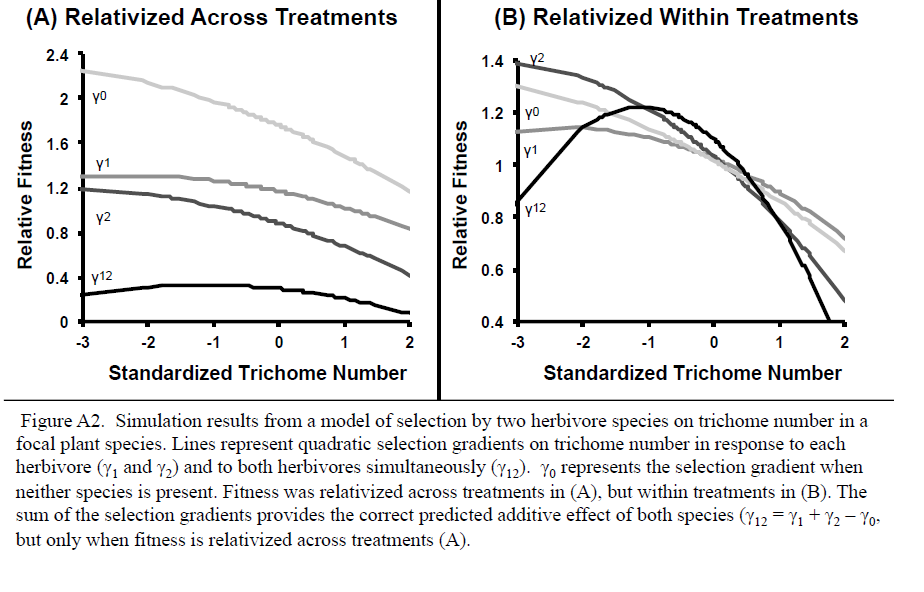
When fitness was relativized across treatments, the simulation revealed weak selection against trichome number when both herbivores were absent (β0 = -0.027) due to the cost of producing trichomes (Fig. A1). There was strong selection for increased trichome number when only Herbivore 1 was present (β1 = 0.074) and weaker selection for increased trichome number when only Herbivore 2 was present (β2 = 0.040; Fig. A2), because trichomes were more effective in reducing damage from Herbivore 1 than Herbivore 2. Recall that Herbivore 1 did not influence the amount of damage from Herbivore 2 (and vice versa), and there was no interaction between the effects of the two herbivores on fitness in our simulation. As a result, there were no indirect ecological effects, and in this case, selection should have been additive. The simulation indicated very strong selection for increased trichome number when both herbivores were present (β1+2 = 0.141), which matches the predicted null hypothesis (β1+2 = β1 + β2 – β0; Supplementary Figure 2A). The simulation indicated that our proposed additive null model (Eq. 3) correctly predicted selection in the presence of both interactors when indirect ecological effects were absent and the selection imposed on the trait by each of the two interactors is independent. We also note that our null model effectively predicted additive selection even when selection was nonlinear; we created a similar simulation model with nonlinear effects of trichome number on plant fitness and found that the additive null hypothesis was also the sum of the quadratic selection differentials (γi) (Supplementary Fig. 2). Here we multiplied quadratic regression coefficients by 2, as per Stinchcombe et al. 2008.
Literature cited
Stinchcombe, J. R., A. F. Agrawal, P. A. Hohenlohe, S. J. Arnold, and M. W. Blows. 2008. Estimating nonlinear selection gradients using quadratic regression coefficients: doubleor nothing? Evolution 62:2435–2440.