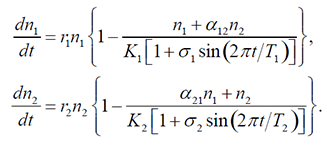Ecological Archives E095-204-A6

Masato Yamamichi, Takehito Yoshida, and Akira Sasaki. 2014. Timing and propagule size of invasion determine its success by a time-varying threshold of demographic regime shift. Ecology 95:2303–2315. http://dx.doi.org/10.1890/13-1527.1

Appendix F. Examples of the simple Lotka-Volterra model.

To demonstrate the generality of our idea, we show the Lotka-Volterra competition model with fluctuating carrying capacities (as Namba and Takahashi 1993),

     (F.1)

where r_i is intrinsic growth rate, K_i is carrying capacity, α_ij is competition intensity of species j on species i, and σ_i and T_i are amplitude and period length of sinusoidal functions. If interspecific competition is strong (K₁ < a₁₂K₂ and a₂₁K₁ > K₂), the system is bistable. In the parameter setting with bistability with symmetrical competitors (r₁ = r₂ = 2, K₁ = K₂ = 90, α₁₂ = α₂₁ = 1.5, σ₁ = σ₂ = 0.5, T₁ = T₂ = 10), establishment success of new species depends on timing of invasion (when propagule size is 50: Fig. F1A, F1B) as well as propagule size (Fig. F1C, F1E). Because two species are completely symmetrical here, minimum density for invasion success is overlapping with population dynamics (Fig. F1E). Note that the per capita growth rate of exotic species is always negative (Fig. F1D), but still invasion is possible with large propagule size.

Fig. F1. A. Invasion success of n₂ when t = 308. Native species (n₁) is shown by dotted line. B. Invasion failure of n₂ (black line) when t = 307. C. Dynamics of A and B in n₁-n₂ plane. D. Per capita growth rate of n₂ and scaled native species density. E. Minimum density required for invasion success at each phase of the cycle. Note that population dynamics of native species (n₁) is overlapping with minimum density of exotic species (n₂).

Literature Cited

Namba, T., and S. Takahashi. 1993. Competitive coexistence in a seasonally fluctuating environment II. Multiple stable states and invasion success. Theoretical Population Biology 44:374–402.

[Back to E095-204]