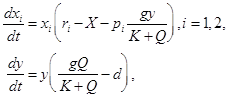 (A.1)
(A.1)
Ecological Archives E095-204-A1
Masato Yamamichi, Takehito Yoshida, and Akira Sasaki. 2014. Timing and propagule size of invasion determine its success by a time-varying threshold of demographic regime shift. Ecology 95:2303–2315. http://dx.doi.org/10.1890/13-1527.1
Appendix A. Examples of the predator–prey model with logistic growth of prey.
According to Yoshida et al. (2007), we introduce Abrams-Matsuda model (Abrams and Matsuda 1997) with logistic growth of prey (xi) and a type II functional response of predator (y),
(A.1)
where X = x1 + x2 and Q = p1x1 + p2x2. This is a generalized model of the classical Rosenzweig-MacArthur model with a single predator feeding on two prey types. Here ri is the intrinsic growth rate of prey i, pi is defense of prey i, g is the maximum growth rate of predator, K is the half saturation rate of predation, and d is predator mortality rate. The model can be rescaled without loss of generality, so that d = p1 = 1 (prey 1 is undefended and prey 2 is defended). We used the same parameter values as Yoshida et al. (2007) for the bifurcation diagram (i.e., g = 2, K = 0.3, and r1 = 1.8). By simulations, we found three types of bistability (Fig. A1), as shown by Abrams (1999). We conducted the same analysis as Fig. 1 and 2 and confirmed that our conclusion regarding invasion timing and propagule size applies to the predator–prey model with logistic growth of prey (Fig. A2–A5).
The bistability 1a (O1/E2: limit cycle with undefended prey and predator vs. stable equilibrium with defended prey and predator) is when p2 = 0.6, r2 = 1.3 (Fig. A2), the bistability 1b (O1/O2: limit cycle with undefended prey and predator vs. limit cycle with defended prey and predator) is when p2 = 0.7, r2 = 1.45 (Fig. A3–A4), and the bistability 2a (O1/E12: limit cycle with undefended prey and predator vs. stable equilibrium with three species) is when p2 = 0.3, r2 = 1.0 (Fig. A5).
Fig. A1. Three bistabilities and a phase diagram of the defense ability (p2) and the intrinsic growth rate (r2) of defended prey in Abrams-Matsuda model. x1 is undefended prey, x2 is defended prey, and y is predator. Parameters of undefended prey are fixed as (p1, r1) = (1, 1.8). Other parameters are d = 1, g = 2, and K = 0.3, which gives a consumer-resource limit cycle when defended prey is absent. The bistability 1a (O1/E2) is when (p2, r2) = (0.6, 1.3), the bistability 1b (O1/O2) is when (p2, r2) = (0.7, 1.45), and the bistability 2a (O1/E12) is when (p2, r2) = (0.3, 1.0) (shown by black points in the phase diagram). Region O1 (x1 oscillation): undefended prey and predator coexist in a limit cycle. Region O2 (x2 oscillation): defended prey and predator coexist in a limit cycle. Region E2 (x2 equilibrium): defended prey and predator coexist in a stable equilibrium. Region E12 (x1 and x2 equilibrium): three species coexist in a stable equilibrium. Region O12 (x1 and x2 oscillation): three species coexist in a limit cycle.
Fig. A2. Effects of invasion timing and propagule size in the bistability 1a (O1/E2) of Abrams-Matsuda model (p1 = 0.6, r1 = 1.3). Introduction at t = 303 (black arrows) results in invasion success and that at t = 308 (gray arrows) results in failure (A, B, C, D).
Fig. A3. Effects of invasion timing and propagule size in the bistability 1b (O1/O2) of Abrams-Matsuda model (p1 = 0.7, r1 = 1.45) when defended prey is invading. Introduction at t = 303 (black arrows) results in invasion success and that at t = 308 (gray arrows) results in failure (A, B, C, D).
Fig. A4. Effects of invasion timing and propagule size in the bistability 1b (O1/O2) of Abrams-Matsuda model (p1 = 0.7, r1 = 1.45) when undefended prey is invading. Introduction at t = 308 (black arrows) results in invasion success and that at t = 303 (gray arrows) results in failure (A, B, C, D).
Fig. A5. Effects of invasion timing and propagule size in the bistability 2a (O1/E12) of Abrams-Matsuda model (p1 = 0.3, r1 = 1.0). Introduction at t = 303 (black arrows) results in invasion success and that at t = 308 (gray arrows) results in failure (A, B, C, D).
Literature Cited
Abrams, P. A. 1999. Is predator-mediated coexistence possible in unstable systems? Ecology 80:608–621.
Abrams, P. A., and H. Matsuda. 1997. Prey adaptation as a cause of predator-prey cycles. Evolution 51:1742–1750.
Yoshida, T., S. P. Ellner, L. E. Jones, B. J. M. Bohannan, R. E. Lenski, and N. G. Hairston Jr. 2007. Cryptic population dynamics: Rapid evolution masks trophic interactions. PLoS Biology 5:e235.