Ecological Archives E095-045-A1

Riin Tamme, Lars Götzenberger, Martin Zobel, James M. Bullock, Danny A. P. Hooftman, Ants Kaasik, and Meelis Pärtel. 2014. Predicting species' maximum dispersal distances from simple plant traits. Ecology 95:505–513. http://dx.doi.org/10.1890/13-1000.1

Appendix A. Overview of the results for linear models to explain maximum dispersal distances using different combinations of plant traits, and histograms of maximum dispersal distance data for different dispersal syndromes and growth forms.

Table A1. Summary of the linear model (R² = 0.51, P < 0.001) showing the effect of dispersal syndrome (DS), growth form (GF), seed mass (SM; mg, log₁₀ transformed), seed release height (RH; m, log₁₀ transformed) and terminal velocity (TV; m/s, log₁₀ transformed) on maximum dispersal distance (m, log₁₀ transformed). The model estimates, t statistics and P values are shown as well as degrees of freedom, F statistics, and P values from a Type II ANOVA. No interactions were found to be significant and the model without interactions is presented. n = 155 species.

Parameters	df	F	P	Estimate	t	P
Type II ANOVA
DS	4	15.56	***
GF	2	1.82
SM	1	0.10
RH	1	2.87
TV	1	7.75	***
Model estimates
Intercept				3.24	9.39	***
DSant				-1.44	-2.43	*
DSballistic				-1.75	-3.28	**
DSwind (none)				-2.76	-7.66	***
DSwind (special)				-2.26	-6.08	***
GFshrub				0.77	1.33
GFtree				0.82	1.50
SM				-0.05	-0.33
RH				0.45	1.70
TV				-1.64	-6.14	***

*** P < 0.001, ** P < 0.01, * P < 0.05

Table A2. Summary of the linear model (R² = 0.61, P < 0.001) showing the effect of dispersal syndrome (DS), growth form (GF), and terminal velocity (TV; m/s, log₁₀ transformed) on maximum dispersal distance (m, log₁₀ transformed). The model estimates, t statistics and P values are shown as well as degrees of freedom, F statistics, and P values from a Type II ANOVA. No interactions were found to be significant and the model without interactions is presented. n = 247 species.

Parameters	df	F	P	Estimate	t	P
Type II ANOVA
DS	4	18.02	***
GF	2	77.56	***
TV	1	73.13	***
Model estimates
Intercept				3.15	9.96	***
DSant				-1.49	-2.77	**
DSballistic				-1.89	-4.03	***
DSwind (none)				-2.65	-8.17	***
DSwind (special)				-2.28	-6.77	***
GFshrub				0.64	1.70
GFtree				1.83	12.45	***
TV				-1.61	-8.55	***

*** P < 0.001, ** P < 0.01, * P < 0.05

Table A3. Summary of the linear model (R² = 0.50, P < 0.001) showing the effect of dispersal syndrome (DS), growth form (GF), seed mass (SM; mg, log₁₀ transformed), seed release height (RH; m, log₁₀ transformed), and terminal velocity (TV; m/s, log₁₀ transformed) on maximum dispersal distance (m, log₁₀ transformed). The model estimates, t statistics and P values are shown as well as degrees of freedom, F statistics, and P values from a Type II ANOVA. No interactions were found to be significant and the model without interactions is presented. n = 264 species.

Parameters	df	F	P	Estimate	t	P
Type II ANOVA
DS	4	35.53	***
GF	2	3.11	*
SM	1	12.77	***
RH	1	9.90	**
Model estimates
Intercept				2.19	10.70	***
DSant				-0.72	-1.73
DSballistic				-1.43	-4.64	***
DSwind (none)				-2.39	-10.03	***
DSwind (special)				-1.03	-4.62	***
GFshrub				0.62	1.78
GFtree				0.76	2.17	*
SM				-0.32	-3.57	***
RH				0.60	3.15	**

*** P < 0.001, ** P < 0.01, * P < 0.05

Table A4. Summary of the linear model (R² = 0.46, P < 0.001) showing the effect of dispersal syndrome (DS), growth form (GF), and seed release height (RH; m, log₁₀ transformed) on maximum dispersal distance (m, log₁₀ transformed). The model estimates, t statistics and P values are shown as well as degrees of freedom, F statistics, and P values from a Type II ANOVA. No interactions were found to be significant and the model without interactions is presented. n = 290 species.

Parameters	df	F	P	Estimate	t	P
Type II ANOVA
DS	4	31.26	***
GF	2	2.48
RH	1	6.10	*
Model estimates
Intercept				2.01	10.34	***
DSant				-0.75	-1.87
DSballistic				-1.39	-4.61	***
DSwind (none)				-2.05	-9.41	***
DSwind (special)				-0.79	-3.90	***
GFshrub				0.73	2.07	*
GFtree				0.48	1.39
RH				0.44	2.47	*

*** P < 0.001, ** P < 0.01, * P < 0.05

Table A5. Summary of the linear model (R² = 0.53, P < 0.001) showing the effect of dispersal syndrome (DS), growth form (GF), and seed mass (SM; mg, log₁₀ transformed) on maximum dispersal distance (m, log₁₀ transformed). The model estimates, t statistics and P values are shown as well as degrees of freedom, F statistics, and P values from a Type II ANOVA. According to Akaike Information Criterion, we found the best model for this data set to include DS:GF interaction (ΔAICc = 28.0 compared to the simple model, model R2 = 0.57, P < 0.001). n = 488 species.

Parameters	df	F	P	Estimate	t	P
Simple model
Type II ANOVA
DS	4	47.34	***
GF	2	46.31	***
SM	1	3.32
Model estimates
Intercept				1.70	12.93	***
DSant				-0.70	-3.45	***
DSballistic				-1.17	-6.17	***
DSwind (none)				-1.76	-11.18	***
DSwind (special)				-0.43	-3.16	**
GFshrub				0.28	1.52
GFtree				1.30	9.56	***
SM				-0.09	-1.82
Model with interactions
Type II ANOVA
DS	4	51.04	***
GF	2	49.93	***
SM	1	2.17
DS:GF	8	5.69	***
Model estimates
Intercept				2.29	12.69	***
DSant				-0.94	-3.40	***
DSballistic				-1.72	-7.37	***
DSwind (none)				-2.39	-11.99	***
DSwind (special)				-1.16	-5.88	***
GFshrub				-0.12	-0.03
GFtree				0.30	1.21
SM				-0.07	-1.47
DSant:GFshrub				-0.33	-0.68
DSballistic:GFshrub				0.31	0.33
DSwind (none):GFshrub				1.50	1.58
DSwind (special):GFshrub				0.73	1.52
DSant:GFtree				-0.32	-0.46
DSballistic:GFtree				0.30	0.53
DSwind (none):GFtree				2.53	3.88	***
DSwind (special):GFtree				1.32	5.19	***

*** P < 0.001, ** P < 0.01, * P < 0.05

Table A6. Summary of the simplest linear model (R² = 0.51, P < 0.001) showing the effect of dispersal syndrome (DS), and growth form (GF) on maximum dispersal distance (m, log₁₀ transformed). The model estimates, t statistics and P values are shown as well as degrees of freedom, F statistic and P value from a Type II ANOVA. According to Akaike Information Criterion, we found the best model for this data set to include DS:GF interaction (ΔAICc = 39.5 compared to the simple model, model R² = 0.55, P < 0.001). n = 576 species.

Parameters	df	F	P	Estimate	t	P
Simple model
Type II ANOVA
DS	4	49.56	***
GF	2	62.09	***
Model estimates
Intercept				1.60	13.83	***
DSant				-0.92	-5.25	***
DSballistic				-1.12	-6.48	***
DSwind (none)				-1.60	-11.63	***
DSwind (special)				-0.32	-2.76	**
GFshrub				0.38	2.40	*
GFtree				1.12	11.14	***
Model with interactions
Type II ANOVA
DS	4	53.90	***
GF	2	67.49	***
DS:GF	8	7.19	***
Model estimates
Intercept				2.30	13.77	***
DSant				-1.31	-5.51	***
DSballistic				-1.78	-8.26	***
DSwind (none)				-2.33	-12.76	***
DSwind (special)				-1.18	-6.51	***
GFshrub				-0.22	-0.66
GFtree				0.05	0.22
DSant:GFshrub				-0.03	-0.07
DSballistic:GFshrub				0.61	0.99
DSwind (none):GFshrub				1.65	1.77
DSwind (special):GFshrub				1.12	2.60	**
DSant:GFtree				0.12	0.21
DSballistic:GFtree				0.44	0.79
DSwind (none):GFtree				2.59	3.97	***
DSwind (special):GFtree				1.48	6.24	***

*** P < 0.001, ** P < 0.01, * P < 0.05

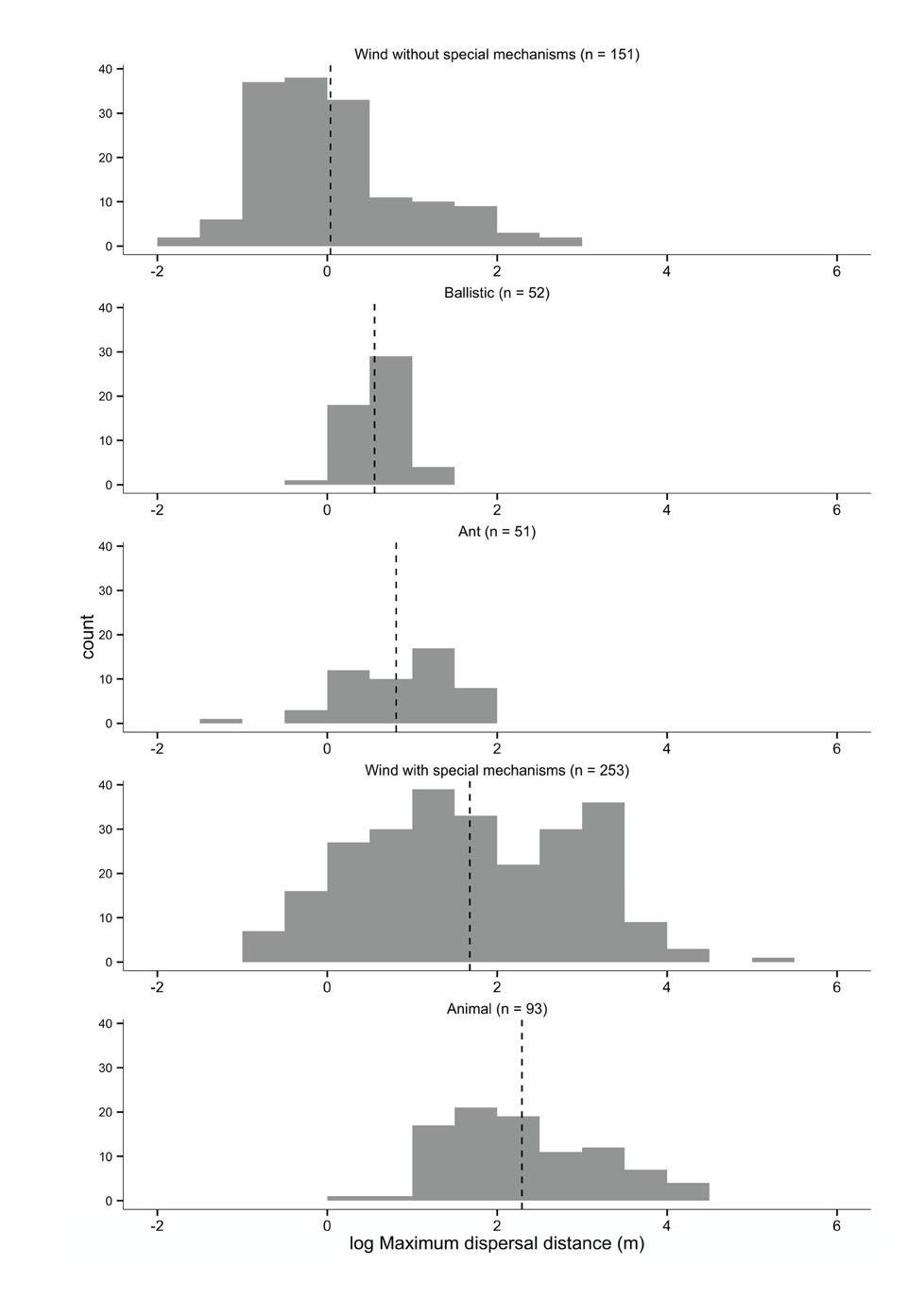
Fig. A1. Histograms of maximum dispersal distance (m, log₁₀ transformed) data for different dispersal syndromes. The dashed vertical lines denote average maximum dispersal distance values for specific dispersal syndromes (1.1 m for wind without special mechanisms, 3.6 m for ballistic dispersal, 6.5 m for ant dispersal, 47.6 m for wind with special mechanisms, 196.0 m for animal dispersal). Total number of species is 576; since some species had maximum dispersal distance data for different dispersal syndromes, 600 data points are used here.

Fig. A2. Histograms of maximum dispersal distance (m, log₁₀ transformed) data for different growth forms. The dashed vertical lines denote average maximum dispersal distance values for specific growth forms (5.2 m for herbs, 24.4 m for shrubs, 295.0 m for trees). Total number of species is 576.

[Back to E095-045]