 .
.
Appendix B. Derivation of uE , the partial derivative of zE and wE with respect to the natural logarithm of time and area, respectively.
Proof:
In Appendix A, we derived Eq. A.8 which stated that:
 .
.
|
(B.1) |
From this equation we will calculate the partial of wE with respect to ln A. The formulation of this partial we will refer to as uE:
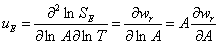 .
.
|
(B.2) |
Before solving for this it is helpful to break Eq. B.1 into three separate functions and derive the partial derivative with respect to A for each function:
 where where
|
(B.3) |
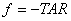 , ,
|
(B.4) |
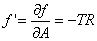 , ,
|
(B.5) |
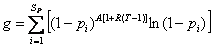 , ,
|
(B.6) |
 , ,
|
(B.7) |
 , and , and
|
(B.8) |
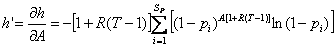 . .
|
(B.9) |
After applying the quotient and product rules to Eq. B.3 we find that:
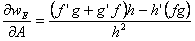 .
.
|
(B.10) |
Finally, uE is calculated by substituting Eq. B.10 into Eq. B.2:
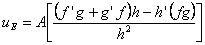 .
.
|
(B.11) |
Unfortunately when equations B.4-B.9 are substituted into Eq. B.11, the resulting formula does not readily simplify, and therefore the final solution is too large to show here in its entirety. By Clairaut's theorem we know that Eq. B.11 will also result from taking the partial of zE with respect to ln T.
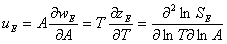 .
.
|
(B.12) |