Jeffrey M. Dambacher, Hiram W. Li, and Philippe A. Rossignol. 2002. Relevance of community structure in assessing indeterminacy of ecological predictions. Ecology 83:1372-1385.

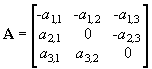
Appendix B. Cramer's Rule and complementary feedback.

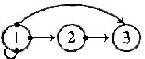
Considering the omnivory system (as in Eq. 12),

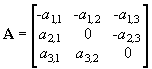(B.1)

we assess the effects to the entire community that results from positive input to a single species through Cramer's Rule (as in Eq. 5). This is accomplished by systematically inserting the column vector [-df_i/dC_h] into the jth column of A and calculating each cofactor of the community matrix. Specifically, we calculate a single cofactor C_3,3 to determine the change (d) in equilibrium abundance of species 3 due to some change in a function (f₃) of its growth rate, as controlled by some parameter C₃. This is within the context of a positive input to variable 3 through a press disturbance or experiment that creates a sustained change to the growth parameter C₃. This sustained change can be, for example, from Mendelian selection that enhances prey capture (e.g., sharper claws), or perhaps experimental supplementation (e.g., food addition to top predator); either of these changes can increase the birth rate of species 3, and thus alter its carrying capacity. The vector [0, 0, -df₃/dC₃] is transposed and inserted into the third column of A in Eq. B.1 to obtain

.

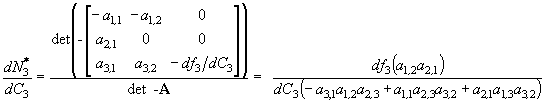(B.2)

The first two elements of the inserted column vector are zero since input here is only through species 3. Inputs through other species can be considered simultaneously by a superposition rule (Nakajima 1992), whereby multiple effects are additive within the inverse matrix, and by extension, the cofactor, adjoint, and absolute feedback matrices (as demonstrated in Fig. 7b). The answer in Eq. B.2 is composed of the C_3,3 cofactor (a_1,2a_2,1), multiplied by the magnitude of the input [df₃/dC₃], and divided by the system determinant (note sign convention of determinant in Appendix A). The result is equal to the corresponding element of the inverse (-A^-1_3,3), and adjoint (adj -A_3,3) matrices. Off-diagonal (i,j) elements of the inverse and adjoint matrices correspond to transposed cofactors (C_ji). The negative community matrix is used in both the numerator and denominator of the left side of Eq. B.2, which maintains a sign convention in both even- and odd-sized systems (as in Eq. 9 and Appendix A).

The insertion of the [-df_i/dC_h] column vector in Eq. B.2 is equivalent to deleting the ith row and the jth column in a cofactor expansion (Appendix A). In terms of the system's linkages, the effect of input is calculated by eliminating all linkages originating in the response variable i, and all linkages terminating in the input variable j. This has the effect of breaking all closed cycles (or loops) having the a_ij linkage, which creates an isolated subsystem. Here the response of variable 3 to input to itself leaves a subsystem that can be depicted either as a matrix minor or signed digraph subsystem

.

(B.3)

Taking the determinant of the A_3,3 minor matrix defines a complementary subsystem that includes variables 1 and 2, the linkages between which comprise the complementary feedback cycle a_2,1a_1,2. This cycle, multiplied by the magnitude of the input [df₃/dC_h], and scaled by the system determinant, defines the equilibrium response of the system (as in the result of Eq. B.2). According to Levins' (1974, 1975) terminology the a_2,1 and a_1,2 linkages graphically define the subsystem that is complementary to the path connecting the input variable j to the response variable i, which in this example is the path from variable 3 to 3. In determinants of off-diagonal minors, however, disjunct cycles are formed that are not entirely composed of complementary subsystems, but include also linkages along the path from variable j to i. In this work however, to avoid new terminology, we have extended the definition of complementary feedback to include all feedback cycles derived from determinants of matrix minors.

Acknowledgments

We thank J. M. Emlen and J. D. Hall for their thoughtful reviews.

Literature cited

Eves, H. 1980. Elementary matrix theory. Dover, New York, New York, USA.

Levins, R. 1974. The qualitative analysis of partially specified systems. Annals of the New York Academy of Sciences 231:123-138.

Levins, R. 1975. Evolution in communities near equilibrium. Pages 16-50 in M. Cody and J. M. Diamond, editors. Ecology and evolution of communities. Harvard University Press, Cambridge, Massachusetts, USA.

Marcus, M., and H. Minc. 1964. A survey of matrix theory and matrix inequalities. Dover, New York, New York, USA.

Minc, H. 1978. Permanents. Encyclopedia of mathematics and its applications. Volume 6. Addison-Wesley, Reading, UK.

Nakajima, H. 1992. Sensitivity and stability of flow networks. Ecological Modelling 62:123-133.