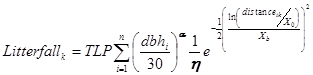
Ecological Archives A025-125-A1

María Uriarte, Benjamin L. Turner, Jill Thompson, and Jess K. Zimmerman. 2015. Linking spatial patterns of leaf litterfall and soil nutrients in a tropical forest: a neighborhood approach. Ecological Applications 25:2022–2034. http://dx.doi.org/10.1890/15-0112.1

Appendix A. Detailed model description and results.

Our approach follows directly from the principles of likelihood estimation (e.g., Edwards 1992, Hillborn and Mangel 1997) and estimates model parameters that maximize the likelihood of observing the actual overall leaf litterfall data for a given target tree species s given the model:

where TLP is the estimated total leaf production of a 30 cm dbh tree of species s, dbhi is the ithtree of N=1….. n neighbors within a 25 m radius of the leaf litter collection basket k, distance is the Euclidean distance between leaf litter trap k and tree i, X₀ is the estimated distance at which the maximum amount of litter is deposited (the mode of the deposition kernel) and X_b determines the estimated spread (variance) of the kernel. Estimated parameter α captures the allometric relationship between tree size and leaf litter biomass production and ƞ is a normalizer. The normalizer scales the dispersion parameter so that TLP is in meaningful units, i.e., the total leaf litter of a 30 cm DBH parent tree. All model parameters (TLP, X₀ , X_b a and α) were estimated separately for each of the 12 species (Table 1).  

Our likelihood function assumes that the residuals, i.e., the difference between observed and predicted leaf litterfall, approximate a normal distribution. Thus, parameter values that maximize the log likelihood will be those that minimize the square deviation between observed and predicted values (as in traditional regression analyses):

We used simulated annealing, a global optimization procedure, to determine the most likely parameters (i.e., the parameters that maximize the log likelihood), given our observed data (Goffe et al. 1994). We ran the algorithm for at least 100,000 iterations and considered it to have converged if it did not change in likelihood in three temperature drops after the initial 50,000 iterations.

Table A1. Species-specific mean parameter values, support intervals, and R² values for estimated dispersal kernels for the 12 target species. See Eq. 1 for parameter description and Fig. 2 for illustration of dispersal kernels for a 30 cm dbh source tree of each of the 12 study species. TLP is the estimated total leaf production of a 30 cm dbh tree, X₀ is the estimated distance at which the maximum amount of litter is deposited (the mode of the deposition kernel) and X_b determines the estimated spread (variance) of the kernel. Parameter α captures the allometric relationship between tree size and leaf litter biomass production

Table A2. Comparison of the proportional contributions of leaf litter inputs observed in the 120 collection baskets and simulated biomass inputs across the entire plot for the 12 focal species.

Literature Cited

Edwards, A. W. F. 1992. Likelihood. John Hopkins University Press, Baltimore, USA

Hillborn, R., and M. Mangel. 1997. The Ecological Detective: Confronting Models with Data. Princeton University Press, Princeton, New Jersey, USA.

[Back to A025-125]