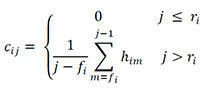Ecological Archives A025-034-A6

Jeffrey F. Bromaghin, Trent L. McDonald, Ian Stirling, Andrew E. Derocher, Evan S. Richardson, Eric V. Regehr, David C. Douglas, George M. Durner, Todd Atwood, and Steven C. Amstrup. 2015. Polar bear population dynamics in the southern Beaufort Sea during a period of sea ice decline. Ecological Applications 25:634–651. http://dx.doi.org/10.1890/14-1129.1

Appendix F. The covariate Cap-procliv used to model heterogeneous recapture probabilities of southern Beaufort Sea polar bears.

Heterogeneity in capture or recapture probabilities is one of the most prevalent violations of mark-recapture model assumptions. The presence of un-modeled heterogeneity in Cormack-Jolly-Seber models causes bias in the estimation of recapture probabilities (Pledger et al. 2003), and therefore in estimates of abundance derived from them using the Horvitz-Thompson estimator (McDonald and Amstrup 2001). Covariates such as indicators of sex and age class, measures of capture effort, and various forms of temporal structure can be used to model capture probabilities and reduce the influence of heterogeneity attributable to known or suspected factors (Lebreton et al. 1992), and we attempted to do so. However, the sufficiency of such covariates for long-lived mammals such as polar bears is uncertain, as their recapture probabilities may depend on individual characteristics such as behavioral tendencies, experiential history, and preferences in habitat or prey.

We developed the recapture heterogeneity covariate Cap-procliv to use an individual's prior capture history as one potential measure of its proclivity to be recaptured in the future, given continued survival. Such an approach could indirectly account for individual characteristics that influence recapture probability, such as behavior, for which it would be impossible to directly obtain quantitative covariates. If fi and ri denote the capture occasions during which individual i was initially captured and first recaptured, respectively, the value of the Cap-procliv covariate for individual i during capture occasion j (cij) was defined as

(F.1)

where was the indicator of capture during occasion m for individual i. The covariate effectively separates individuals into two categories for each capture occasion, those that have and have not been previously recaptured. In that sense, the covariate is a generalization of the "transient" concept that has become common in mark-recapture models (e.g., Pradel et al. 1997, Conn et al. 2011, Smout et al. 2011). Beginning with an individual's first recapture, the covariate incrementally accumulates knowledge of an individual's tendency to be captured as a mark-recapture investigation proceeds through time. Note that the value of Cap-procliv for occasion j utilizes capture information from occasions prior to j only, and is therefore independent of the capture event at occasion j. The capture history of an adult male polar bear from the southern Beaufort Sea and the resulting Cap-procliv covariate are provided as an example (Table F1).

Table F1. An example of the recapture heterogeneity covariate Cap-procliv for an adult male polar bear captured five times from 2001 to 2010.

 

The influence of the Cap-procliv covariate on recapture probability estimates was illustrated by comparing the parameter estimates of two nearly identical models based on the USGS data set. The first model, which included Cap-procliv, had the minimum value of AIC among the suite of models considered, and the second model contained the same parameters excepting Cap-procliv. Estimates of the parameters of the model including Cap-procliv are consistently smaller (Fig. F1) than the estimated parameters of the model excluding the covariate (Fig. F2). This was expected, as the structure of the covariate allows the estimated recapture probabilities of individuals caught frequently to increase (reducing their negative bias), and the estimates for individuals caught less frequently to decrease (reducing their positive bias). In addition, the AICC values in the two models differed by 16, which reflects the improved model fit the covariate provided. As an additional example, the estimated recapture probabilities for an adult male with the capture history in Table F1 obtained from the two models are presented in Fig. F3. In the model including Cap-procliv, recapture probabilities for this individual are reduced from 2002 to 2005, compared to the model excluding the covariate. It was first recaptured in 2005, after which its recapture probability is elevated from 2006 to 2010 relative to the model without Cap-procliv. The additional flexibility to model heterogeneity in recapture probabilities is expected to reduce negative bias for individuals captured frequently and positive bias for individuals captured infrequently.

 

Fig. F1. Partial output of the function F.cjs.estim from the R package mra for the example model including the covariate Cap-procliv.

---

 

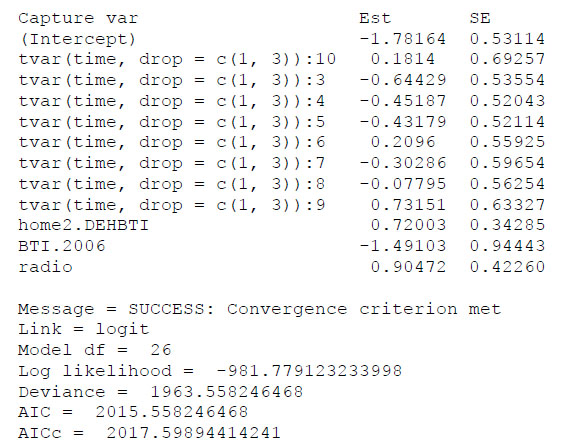
Fig. F2. Partial output of the function F.cjs.estim from the R package mra for the example model excluding the covariate Cap-procliv.

---

 

Fig. F3. Estimated recapture probabilities for an adult male bear in the USGS data set with the capture history in Table F1 and a home stratum of Deadhorse, Alaska, based on models that were identical except for their inclusion of the recapture heterogeneity covariate Cap-procliv. The value of the Cap-procliv covariate for this individual in each year (Table F1) is shown as a fraction immediately above the horizontal axis.

---

 

The influence of the Cap-procliv covariate on estimates of abundance was assessed by comparing model-averaged estimates of abundance obtained from the USGS data set with and without use of the covariate. Estimates of abundance obtained using the Cap-procliv were obtained from the original analysis of the USGS data set. The covariate was eliminated from each model, the parameters of each model were re-estimated, and the resulting estimates of abundance were averaged over the model set. The difference between the two time series of abundance estimates (Fig. F4) was consistent with expectations (Carothers 1973, Pledger et al. 2010). The increased flexibility to indirectly model unknown sources of heterogeneity in recapture probabilities appears to have reduced bias in abundance estimates. The covariate allowed the smaller subset of individuals captured frequently to have increased recapture probabilities and decreased their contribution to the Horvitz-Thompson abundance estimates (McDonald and Amstrup 2001). Coincidently, estimated recapture probabilities for the larger subset of individuals captured less frequently decreased, which increased their contribution to the abundance estimates. The net effect was a reasonably consistent increase in the annual abundance estimates, averaging 17% across all 9 years (Fig F4).

 

Fig. F4. Model-averaged estimates of annual abundance, with and without use of the recapture heterogeneity covariate Cap-procliv, based on the USGS data set.

---

Methods of modeling individual heterogeneity in probabilities of capture and survival remains an area of active interest in mark-recapture applications because of the estimation bias unexplained heterogeneity can cause (e.g., Abadi et al. 2013). Random effect (Royle 2008) and mixture (Pledger et al. 2010) models are two approaches that have gained widespread utilization. The covariate Cap-procliv we introduced provides an additional option that directly utilizes information in the capture histories of individual animals, which record the ultimate effects of heterogeneity, and is easy to implement in Cormack-Jolly-Seber models using the standard covariate approach (Lebreton et al. 1992). The covariate performed as expected in this application, appearing to appropriately counteract bias of known direction in both recapture probabilities and abundance estimates. The comparative merits of alternative methods of accounting for heterogeneity in recapture probabilities are difficult to assess with a data set resulting from a single realization of a mark-recapture experiment. For that reason, a simulation to investigate the performance of this approach under known conditions is planned.

 

Literature cited

Abadi, F., A. Botha, and R. Altwegg. 2013. Revisiting the effect of capture heterogeneity on survival estimates in capture-mark-recapture studies: Does it matter? PLoS ONE 8:e62636.

Carothers, A. D. 1973. The effects of unequal catchability on Jolly-Seber estimates. Biometrics 29:79–100.

Conn, P. B., A. M. Gorgone, A. R. Jugovich, B. L. Byrd, and L. J. Hansen. 2011. Accounting for transients when estimating abundance of bottlenose dolphins in Choctawhatchee Bay, Florida. The Journal of Wildlife Management 75:569–579.

Lebreton, J. D., K. P. Burnham, J. Clobert, and D. R. Anderson. 1992. Modeling survival and testing biological hypotheses using marked animals - a unified approach with case-studies. Ecological Monographs 62:67–118.

McDonald, T. L., and S. C. Amstrup. 2001. Estimation of population size using open capture–recapture models. Journal of Agricultural, Biological, and Environmental Statistics 6:206–220.

Pledger, S., K. H. Pollock, and J. L. Norris. 2003. Open capture-recapture models with heterogeneity: I. Cormack-Jolly-Seber model. Biometrics 59:786–794.

Pledger, S., K. H. Pollock, and J. L. Norris. 2010. Open capture-recapture models with heterogeneity: II. Jolly-Seber model. Biometrics 66:883–890.

Pradel, R., J. E. Hines, J. Lebreton, and J. D. Nichols. 1997. Capture-recapture survival models taking account of transients. Biometrics 53:60–72.

Royle, J. A. 2008. Modeling individual effects in the Cormack-Jolly-Seber model: A state-space formulation. Biometrics 64:364–370.

Smout, S., R. King, and P. Pomeroy. 2011. Integrating heterogeneity of detection and mark loss to estimate survival and transience in UK grey seal colonies. Journal of Applied Ecology 48:364–372.

---

[Back to A025-034]